In powertrain systems, all deformable elements can dissipate energy when subjected to dynamic deformations. The internal damping of these elements including bearings and supports, shafts, and gears have an important impact on the energy dissipation. Consequently, damping plays an important role in the design of structures to minimize noise, structural instability, and fatigue failure of components. The gear meshing damping is known as an important determinative factor in the dynamic response of the system under specific running conditions. Without damping, undesirable induced vibrations create noise, increase dynamic loads, and potentially damage the gear teeth and bearings. It is well-known that plastic materials have higher damping values than steel. So, the main question discussed in this paper is, how noise, vibration, and harshness (NVH) are influenced by the presence of different viscous gear meshing damping. Here, some guidelines are presented to adjust the gear meshing damping for achieving the NVH characteristics of a powertrain system. In this regard, a dynamic calculation process called “forced response analysis tool” has been developed in KISSsoft to enable analysts and engineers to perform the dynamic analysis of the powertrain systems quickly and efficiently (Refs. 1, 2). To achieve this goal, gear body material with higher damping properties within the required torque ratio specifications can be chosen. Based on the static transmission error of the gears, shaft imbalances, etc., the bearing reaction forces are calculated by considering their mass and inertia.

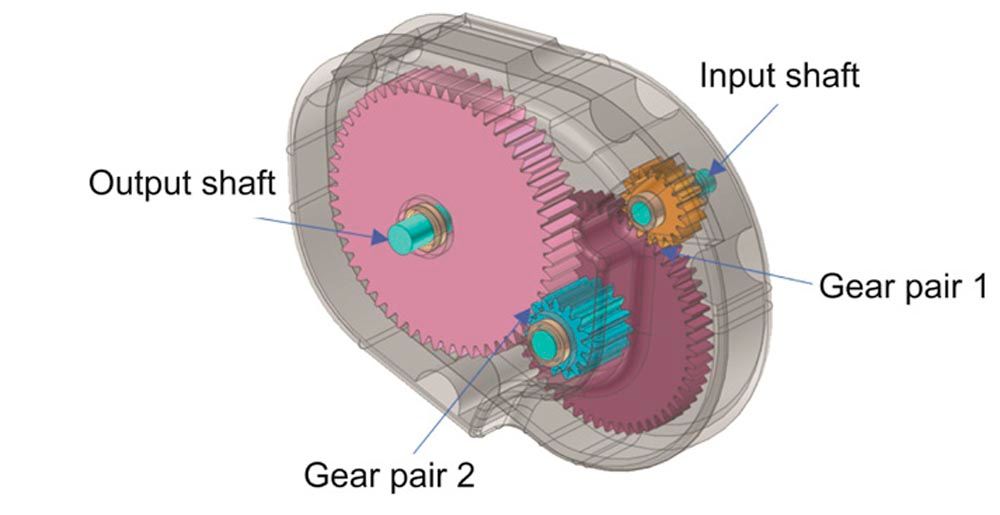
Figure 1—A two-stage gearbox model layout.

Forced Response Analysis

A two-stage gearbox model is considered in two variants with different gear materials, one with plastic gears and one with steel gears, see Figure 1. Both variants have the same input parameters (load, speed, number of cycles) and are designed to have similar root and flank safety. Therefore, the plastic gears are larger and have bigger diameters. The plastic gears’ strength is calculated according to VDI 2736, while the steel gears’ strength is calculated using ISO 6336. Both variants have the same housing material. Based on the load excitation imposed by the gears, the forced response analysis is conducted and at the bearing positions, the transient loads are evaluated.

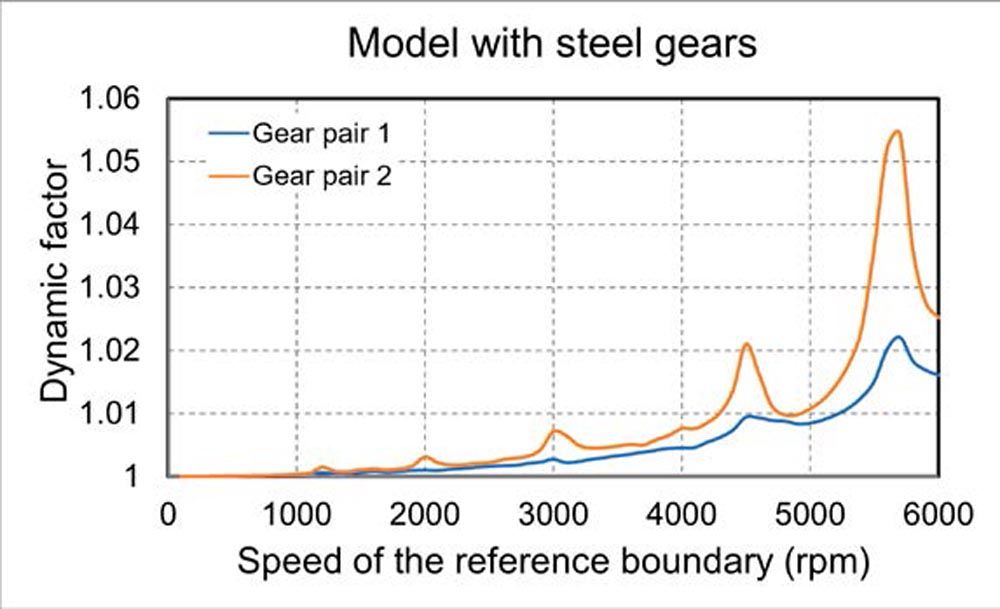
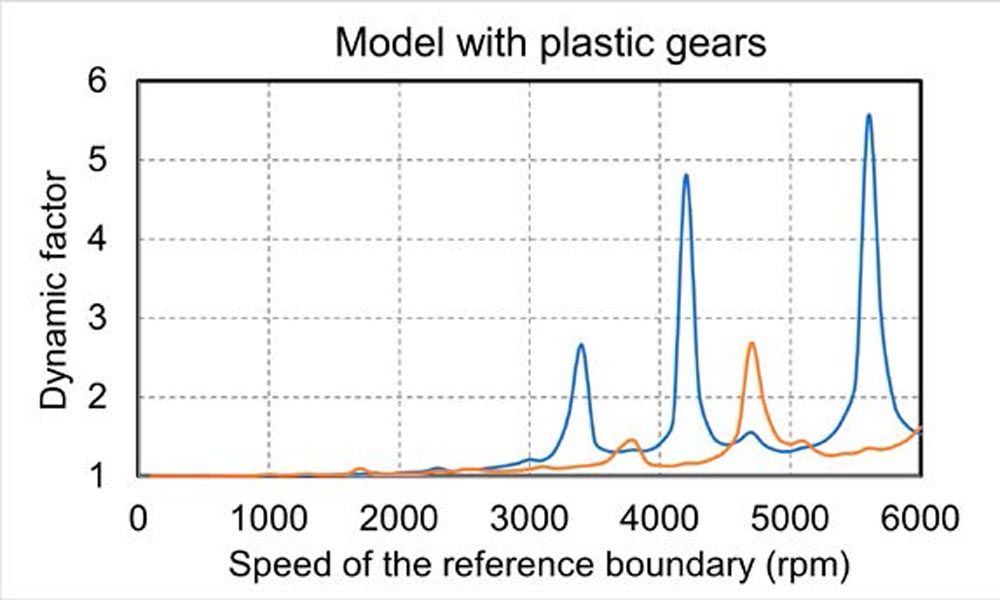
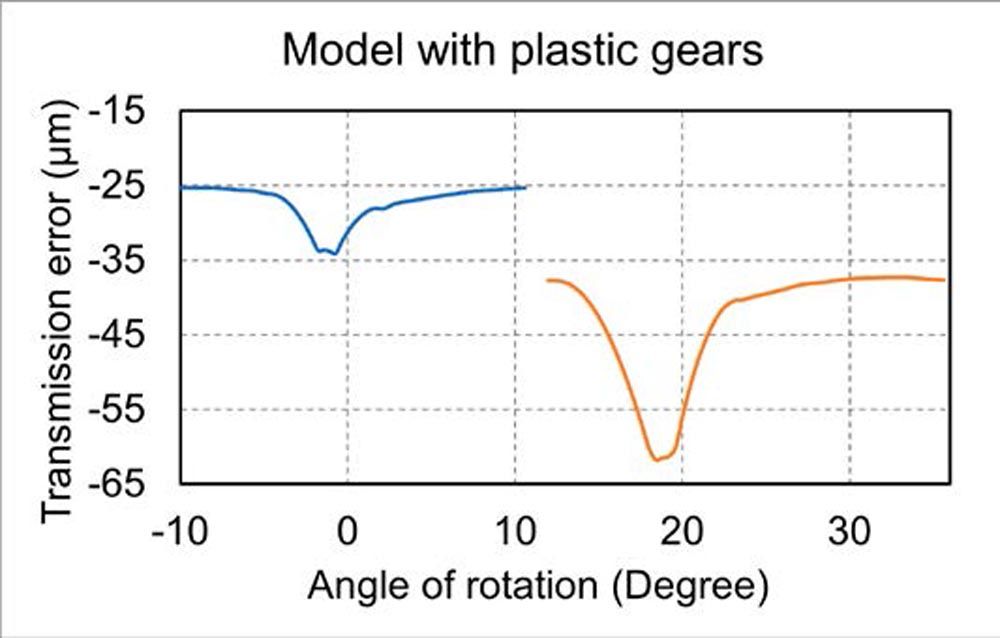
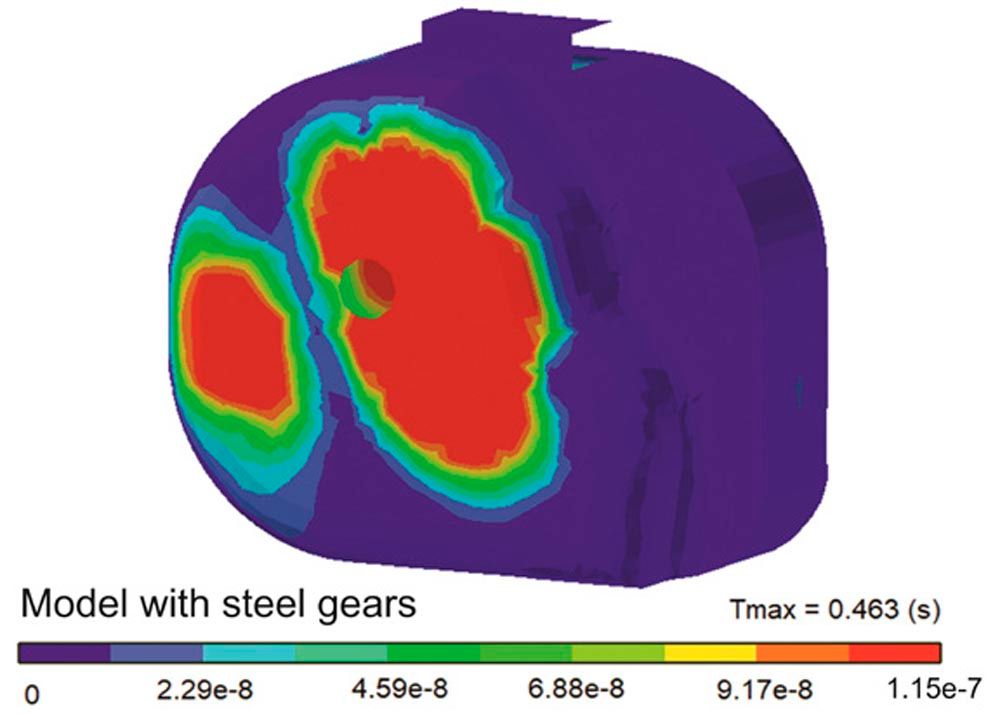
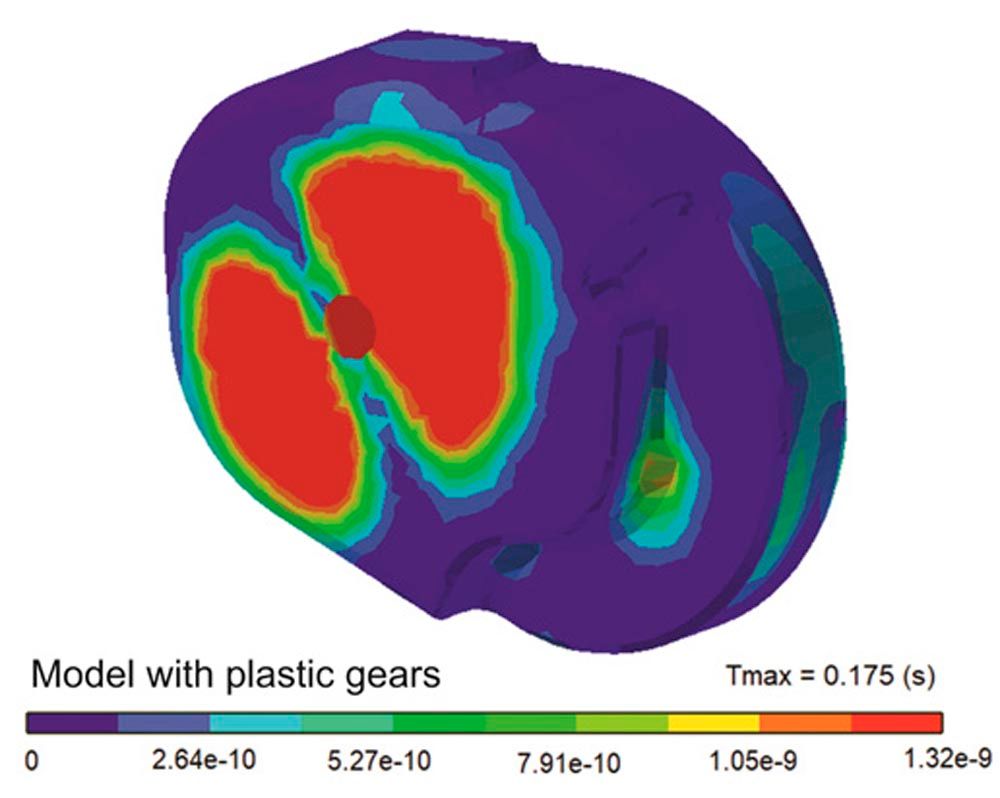
In the first step of the forced response analysis, the dynamic factor K_v is evaluated. The dynamic factor is the ratio of the maximum dynamic excitation load between the meshing gears to the static contact force. K_v of the first gear pair of both models without gear meshing damping is shown in Figure 2. The dynamic factor characterizes the system behavior under dynamic loading at different shaft speeds and reveals the margins of the operational speeds for which the powertrain system can be significantly excited. The increase of the dynamic factor in the model with plastic gears is much higher than in the other model when no gear meshing damping is considered. The main reason behind this difference is the high transmission error due to the low meshing stiffness of the plastic gears compared to the steel gears, see Figure 3. In the example used, the dynamic meshing forces of the plastic gear model without damping consideration increased up to 550 percent (K_v=5.5); whereas in the steel gear model, the increase is only about 5.5 percent (K_v=1.055) (Fig. 2). When we first obtained these results, we were searching for errors in the calculation approach, as—from practice and test rigs—we know that gear drives with plastic gears have lower excitations. However, the results changed completely when we rerun the calculations considering damping.

Figure 2—Dynamic factor without gear meshing damping, d=0 Ns/m.

Figure 3—Transmission error of the gear pairs.

When considering the damping effect in the meshing, the effect on the dynamic meshing contact forces for the gearbox with steel gears is noticeable, decreasing in our example K_v from 1.055 to 1.020, see Figure 4. Note that a damping factor d=1,000 Ns/m is a good approach for steel. In the model with plastic gears, the damping decreased the dynamic factors dramatically; in our example, K_v came down from 5.500 to 1.015 with a damping factor d=1,000 Ns/m (and to 1.004 with d=5,000 Ns/m). It is difficult to obtain precise damping factors for plastic materials. After extensive research of the available literature, we determined the damping factor depends on the plastic type, temperature, and fiber reinforcement and that a damping factor of d=5,000 Ns/m is a conservative assumption to use.

Figure 4—Dynamic factor of the models with different gear meshing damping.

It is interesting to notice that the effect of damping already at low values is dominant, which means that the reduction of the dynamic factor from d=0 Ns/m to 1,000 Ns/m is higher than the reduction from 1,000 Ns/m to 5,000 Ns/m. The same conclusion can be drawn by comparing the dynamic factor reduction from successive damping increases. As the main conclusion from the above analysis, it reveals that for plastic gears, an analysis without damping is useless. This implies that the damping should not be neglected even when a very approximate damping factor must be used, otherwise it would lead to an unrealistic response of the system.

NVH Analysis in RecurDyn Based on the Forced Response Analysis in KISSsoft

When executing an NVH evaluation, the gearbox housing is excited by the transient bearing forces at the bearing location points, and consequently, the noise emitted from the housing is evaluated. The bearing forces calculated in KISSsoft are imported to RecurDyn and applied directly to the housing of the powertrain model at bearing positions. As a major kinematic parameter required for the NVH analysis, the surface velocities at nodes of the meshed geometry are calculated. Finally, the equivalent radiated power (ERP), as the main factor for measuring the emitted noise level from the housing`s surface to the environment, is calculated. To demonstrate which parts of the housing’s surface emit higher noise, the contour plot of the ERP is very helpful. It can subsequently be used to address demanded design modifications, such as local stiffening of the housing utilizing the ribs, to reduce the noise. Based on the bearing reaction forces calculated in the forced response at a speed of 5,600 rpm, the ERP contours of both models are shown. In both models, the region of the housing close to the output shaft has higher ERP values, and consequently, emits noise to the environment. The plastic gears model has a much better performance concerning noise emission. The difference between the scales of the ERP of both models reveals this superiority (Figure 5). The maximum values of the color legends are adjusted to clearly show the noise distribution through the housing’s surface. It is noticeable to mention that the variation of the ERP depends on the simulation time and the locally evaluated position on the housing.

Figure 5—ERP contours at the time with maximum values at a speed of 5,600 rpm.

Conclusion

This paper presented some steps to get more insight into the effect of meshing damping on the dynamic response and noise emission of a two-stage gearbox transmission system. For this purpose, two variants of the model with different gear materials, one with plastic gears and one with steel gears, were considered. Both variants were designed for the same number of cycles of operation with similar root and flank safeties. The forced response analysis of the models was carried out and the exciting reaction bearing forces were calculated to evaluate which model can achieve better NVH characteristics results with lower noise emission from the housing. It was observed that for plastic gears, the damping should not be neglected even when using an approximate damping value, otherwise it would lead to the unrealistic response of the system. Therefore, for plastic gears, consideration of meshing damping by selecting suitable gear material can be an efficient approach for damping undesirable induced vibrations. On the other hand, for steel gears, it is not as crucial as for plastic gears to use damping, since the results are less affected when compared to the plastic gears.

References

1. Ebrahimi, S.; Langhart, J.; Marano, D.: “NVH Calculations for Drivetrains, A Methodology for Selection of the Best Suitable Calculation Approach for a Specific Purpose,” International Conference on Gears 2022, Technical University of Munich (TUM), VDI Verlag.
2. KISSsoft User Manual, KISSsoft AG., Bubikon, Switzerland, 2023.