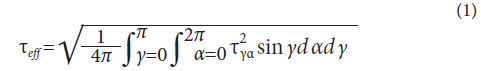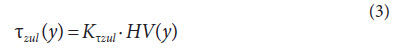Tooth Flank Fracture - Basic Principles and Calculation Model for a Sub-Surface-Initiated Fatigue Failure Mode of Case-Hardened Gears

Tooth Flank Fracture – Basic Principles and Calculation Model for a Sub-Surface-Initiated Fatigue Failure Mode of Case-Hardened Gears

Dipl.-Ing. I. Boiadjiev, Dr.-Ing. J. Witzig, Dr.-Ing. T. Tobie and Prof. Dr.-Ing. K.Stahl

Cracks initiated at the surface of case-hardened gears may lead to typical life-limiting fatigue failure modes such as pitting and tooth root breakage. Furthermore, the contact load on the flank surface induces stresses in greater material depth that may lead to crack initiation below the surface if the local material strength is exceeded. Over time the sub-surface crack propagation may lead to gear failure referred to as “tooth flank fracture” (also referred to as “tooth flank breakage”). This paper explains the mechanism of this subsurface fatigue failure mode and its decisive influence factors, and presents an overview of a newly developed calculation model.

Introduction

Case-hardened gears are highly loaded machine elements used for power transmission in many field applications. But one factor that can limit the life cycle of such highly loaded gears is load-carrying capacity. To ensure safe operation of these gears, reliable calculation and test methods are needed. With a variation in material type and heat treatment parameters, it is possible to influence the flank load-carrying capacity. Extensive theoretical and experimental investigations have been carried out in order to derive calculation methods and an optimized heat treatment — mostly for the fatigue failure pitting mode that occurs as a result of cracks initiated at or just below the flank surface. What is more, in many field applications of highly loaded, case-hardened gears, failures also occur due to primary crack initiation deep below the material surface. Affected are not only casehardened cylindrical gears but also bevel and hypoid gears for different applications. Such failures were also found in nitrided and induction-hardened gears. The consequence of such failures with crack initiation below the flank surface is, in almost all cases, the spontaneous and complete loss of drive of the affected gear set. Because the crack propagates below the surface, it is almost impossible to detect at an early stage with visual inspections. Whether a failure occurs at the surface or at greater material depth, it is influenced by local contact load that depends on the gear flank geometry — in particular the equivalent radius of curvature — and by the local material strength. The in-depth strength of the material results primarily due to heat treatment. To predict a failure, the load curve has to be set in relation to the strength curve over the material depth. On gear sets with relatively small equivalent radius of curvature, the maximum Hertzian stress occurs relatively near the surface. Furthermore, the influences of oil and surface roughness should be taken into account, as they can lead to a substantial increase of the local loads in this area. Under the condition of constant Hertzian stress, a larger equivalent radius of curvature results in shifting the maximum Hertzian stress towards a larger material depth stresses in greater material depth, whereas the influences on the flank surface remain nearly the same. If the material strength below the surface is exceeded due to these shifted stresses, a crack can be initiated in this area. With time the crack propagation through the material may result in a gear failure sometimes referred to as “tooth internal fatigue fracture” (TIFF), tooth flank fracture or subsurface fatigue that can eventually lead to the total damage of the gear set. Such sub-surface fatigue failures were observed — even at loads below the rated allowable ones based on standard calculation procedures for pitting and bending strength. This fact indicates a different failure mechanism. There was so far basically no common understanding about the failure mechanism and its influence factors. Furthermore, due to lack of consequent investigations, there was no adequate calculation method present, so the risk of tooth flank fracture could not be quantified. For this reason, investigations in the field of subsurface fatigue were of a great importance.

In recent years extensive theoretical and experimental investigations have been conducted in order to achieve a better understanding of the failure mechanism and to isolate the decisive influence factors on the failure mode of tooth flank fracture. From the results of these investigations a calculation method was derived that allows the evaluation of the material exposure — not only at the loaded flank surface — but also in greater material depth. The model sets the in-depth shear stress, resulting from the Hertzian load on the flank surface in relation to the local material strength, which is directly derived from the local hardness profile. In this way a local material exposure for every volume element below the surface can be calculated. Based on gear geometry, operating conditions, and material properties — which also include the residual stresses as a decisive influence parameter — the risk of sub-surface fatigue failure can be determined.

Failure Mechanism of Tooth Flank Fracture

At the Gear Research Center (FZG), ongoing investigation leads to a computer- based method for calculating transmission error and dynamic tooth force based on measured flank topology (Ref. 4); this method is used in a comparison with noise measurement for automotive transmissions. The presented methodology enables the gear engineer to optimize the microgeometry with respect to robust manufacturing.

Figure 1 Typical surface gear failure examples – pitting (left) and tooth root breakage (right)
- Click image to enlarge

Figure 2 Examples of tooth flank fracture – test gear from (19) (left), turbine gear from (2) (right)
- Click image to enlarge

Gears with tooth flank fracture show characteristic features that differentiate them from gears that failed due to pitting, micropitting or tooth root breakage. For example, Figure 1 shows two gears that failed due to pitting and tooth root breakage, which have in common the fact that the crack was initiated at or close to the surface. Figure 2 shows two example gears — a test and a turbine gear — with tooth flank fracture. These are only two examples, among many others, showing that sub-surface fatigue failures, such as tooth flank fracture, can occur in almost every field application. Failures due to tooth flank fracture are reported in wind and steam turbines, truck gearboxes, bevel gears for heavy machinery, and test gearboxes. Typical failure mode for tooth flank fracture is that the crack initiation is normally located below the flank surface in an approximate depth of the case-core transition (Fig. 3a and b) in the active flank area. The primary crack is often initiated at non-metallic inclusions that have significantly different Young’s modulus compared to the normal material structure. Such imperfections below the surface act as stress risers during the roll off of the flank because of the notch effect. If the material strength is locally exceeded, a crack with growth potential could be initiated in the material that can lead to tooth flank fracture later.

Figure 3 Characteristic features of tooth flank fracture (19)
- Click image to enlarge

After a crack has been initiated below the surface, it slowly propagates during operation in an angle of 40° to 50° relative to the flank surface — but without direct connection to the surface. During the crack propagation a so called “fish eye” can occur due to relative microscopic movement of the cracked surfaces. The primary crack propagates from the crack starter towards the surface of the loaded flank, and into the tooth core towards the opposite tooth root section. The crack propagation rate towards the loaded flank is smaller in comparison to the core, due to the higher hardness. After the primary crack has grown enough so the tooth stiffness is reduced, secondary cracks may occur under load. A distinctive feature of these cracks is that they normally start at the flank surface and propagate parallel to the tooth tip into the material. As shown in Figure 3a) and b), after the secondary crack meets the primary one, particles from the active flank might break out. As the main crack reaches the that carries the load is rapidly decreased. When a critical crosssection is reached, the upper tooth piece is separated from the gear. The final breakage of the tooth is due to overload breakage (Fig. 3c). On the fracture area, a typically shiny crack lens around the crack starter and a zone of rough overload breakage can be observed (Fig. 3c and 3d). Due to the given characteristics, the failure type of tooth flank fracture can be differentiated from other failure types such as tooth root breakage and tooth interior fatigue fracture (TIFF) that show a crack progression over the tooth cross-section as well. The failure type of tooth root breakage is characterized by a crack in the 30°-tangent area on the tooth root fillet. According to (Ref. 3) the load on the tooth leads to a complex, multi-axial stress condition. The bending stress in the tooth root changes over time when the load on the flank moves towards the tooth tip or the tooth root, respectively. Due to the bending moment, stresses in the tooth root cross-section are induced, which are tensile on the loaded and compressive on the unloaded flank side. These stresses have their maximum at the surface, so the risk of a crack initiation is greatest there. The two main differences between the failure modes of tooth flank and tooth root breakage are location of the failure in tooth height direction and location of the initial crack. The typical endangered area for tooth flank fracture can be found at half tooth height of the active flank, whereas tooth root breakage normally occurs below the active flank in the 30°-tangent area on the tooth fillet. Furthermore, the crack initiation of the tooth root breakage happens mostly at, or just below the surface, and not in greater material depth like the initial crack of the tooth flank fracture. The failure type of tooth interior fatigue fracture is most common on gears with alternating loads, where both tooth flanks are used to transmit torque. A characteristic feature of TIFF (Fig. 4) is that the crack propagation path runs nearly parallel to the tooth tip surface with small drops near the surface. The causes for TIFF are not only the alternating loads on both sides on the tooth, but also the tensile residual stresses in the tooth core resulting from the heat treatment. Also typical for TIFF is that the upper tooth segment is normally separated along a plateau at half tooth height.

Figure 4 Schematic visualization of tooth interior fatigue fracture (TIFF).
- Click image to enlarge

Influence Factors on the Failure Type Tooth Flank Fracture

General stress conditions in the tooth. The induced stresses inside the loaded tooth are shown in Figure 5. Considering an ideal, smooth flank surface, the general stress condition inside the tooth is composed of following components:

• Stresses due to the normal force resulting from the transmitted torque
• Shear stresses on the flank surface due to friction
• Thermal stresses caused by the thermal gradient
• Bending stresses and shear stresses due to shear load caused by the normal force
• Residual stresses

Figure 5 Stress conditions inside the tooth (19).

Figure 5 shows the stress components acting in a considered element below the surface. In Figure 5a) the stress distribution due to the normal force is shown, where the contact stress can be described according to the Hertzian theory. The effects of the relative sliding between the two gear flanks are considered with the friction force. Figure 5b illustrates the bending stress distribution over the tooth cross-section. Due to the normal force, tensile stress is induced on the side of the loaded flank and compressive stress on the back flank. In comparison to the bending stress, which is nearly linear over the tooth cross-section, the stresses due to shear load can be approximated by a parabolic distribution with a maximum at the middle of the tooth. In Figure 5d the residual stresses are shown. As a result of the heat treatment, compressive stresses normally occur in the case area, and are compensated by tensile stresses in the tooth core. Unlike the stresses in 5a, b and c, the residual stresses are load-independent and constant over time if the load is not too high. The residual stresses and the load induced stresses can be superimposed if the different time dependence of the stress components is considered.

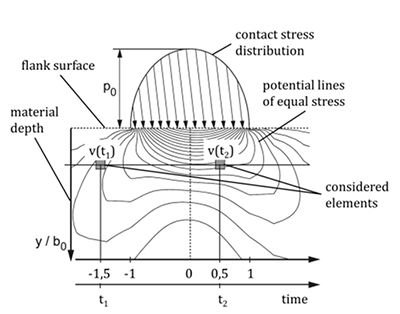
Figure 6 Time-dependent stress in the rolling contact (7).

Stress conditions in the rolling contact. On a loaded tooth flank the rolling direction × can also be seen as the time axis. For each considered element in the material the stress conditions change due to the relative motion of the mating tooth flanks. Figure 6 illustrates schematically the rolling contact with the induced stress (one component of the 3-axis stress condition) below the surface. Under the assumption of constant equivalent radius of curvature and normal force, all volume elements in the same material depth are exposed to equal stresses, but at different times during the roll-over process. Furthermore, a single volume element is subjected to different stresses at different times, so when the material exposure is calculated in a considered element below the surface, the stresses have to be considered over the whole time axis (x-axis). However, the difficulty in this observation is the turning of the principal coordinate system during the rolling contact, resulting in a variation of the absolute stress values as well as the direction of the principal stresses for each volume element. The stress distribution over the material depth is mainly influenced by the maximum Hertzian pressure p0 resulting from the Hertzian contact load and the local equivalent radius of curvature ρc. As shown in Figure 7, the shear stress τH below the surface increases with an increasing equivalent radius of curvature ρc — even if the maximum contact pressure p0 and maximum shear stress τH remain the same. Because the relative radius of curvature increases not only with increasing center distance, but also with increasing pressure angle or increasing addendum modification factor, an increased shear stress τH below the surface can be expected in these gear configurations. Furthermore, based on the fact that the local strength profile derived from the hardness profile remains constant, the remaining strength reserve erodes and the risk of a crack initiation below the surface increases.

Figure 7 Influence of the equivalent radius of curvature on the shear stress below the surface (19).

Multi-axial stress conditions are commonly described by means of equivalent stresses. Theoretical investigations in (Ref. 7) have shown that many of the common equivalent stress hypotheses, such as the distortion energy hypothesis, shear stress hypothesis and alternating shear stress hypothesis, are not suitable for alternating stresses and stress conditions with a rotating principal coordinate system. In (Ref. 7) various hypotheses are discussed to their applicability for rating the material exposure in rolling contacts. In (Ref. 7) it could be shown that the so called shear stress intensity hypothesis (SIH) is applicable to loaded rolling contacts. The shear stress intensity τeff can be calculated according to Equation 1; it considers all maximum shear stresses τγα in each sectional plane γα of the considered volume element.

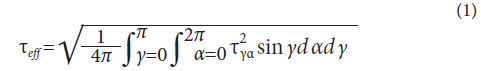
Local material strength. Another decisive influence factor, beside the stress conditions in the rolling contact, is the local material strength limiting the load carrying capacity. Tooth flank fracture can occur if the material strength below the surface is exceeded. According to (Ref. 7) the material strength can be determined based on material-physically relations where the local strength values are calculated out of the local Vickers hardness. An alternative, simpler method is used in (Refs. 6; 12–14; 16; 19) where the material strength is assumed to be directly proportional to the local hardness. Further influences due to grain size and segregation cannot be considered by the actual state of the art.

Calculation Model

Basic formulae. A calculation model was developed at FZG to determine the risk of tooth flank fracture. The model considers different volume elements below the surface to determine the local material exposure as a comparison of the local occurring equivalent stress and the local strength that is derived from the hardness profile. Using Equation 2, the occurring local stress based on the equivalent stress according to the shear stress intensity hypothesis (SIH) can be calculated:

Both τeff, Last, ES and τeff, ES can be calculated using Equation 1. However, different stress components are considered. For the calculation of τeff, Last, ES all stress components due to external loads as well as components due to residual stresses are used, whereas the determination of τeff, ES is done only with the quasi-static residual stresses. Basically the decisive equivalent stress τeff, DA can be taken as an oscillating stress with the double amplitude (Eq. 2). For the calculation of the material exposure besides the occurring local stress, the local strength derived from the hardness profile below the surface is required:

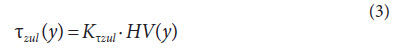
Although there is no generally valid relation between the permissible shear strength and the local hardness, simplified it can be assumed that the material strength, especially on case-hardened gears, is directly proportional to the local hardness. The factor describing the linear relation between the Vickers hardness and material strength has a constant value of 0.4, which was derived from gear running tests and results from industry gearboxes. This value is valid for case-carburized gears made of typical case-hardening steels and with adequate heat treatment. With τeff, DA and τzul the material exposure AFB for each volume element below the surface can be determined according to (Ref. 19) using Equation 4:

With the calculation of the material exposure AFB over the material depth at different points from the tooth root towards the tooth tip the risk of tooth flank fracture can be evaluated for different mesh positions considering the local equivalent radius of curvature, the local contact pressure and the local hardness. The limit for the material exposure AFB, above which tooth flank fracture should be expected, was set to 0.8. This critical value was derived from gear running tests on test gears and recalculation of gearboxes from different industry applications.

Figure 8 Comparison of the calculated material exposure curves for two example gearboxes (19).

Figure 8 shows the comparison of two calculated material exposure curves for two example gearboxes. The material exposure maximum AFB, max for gearbox 1 is reached near the surface, whereas the maximum exposure AFB, max for gearbox 2 can be observed in greater material depth. The location of the peak is mainly influenced by the equivalent radius of curvature, by the occurring contact loads and by the heat treatment parameters. Depending on the location of the maximum material exposure, the failure type can be predicted. High material exposure values at the surface indicate pitting whereas material exposure peaks in greater depth can be interpreted as at high risk of tooth flank fracture. Figure 9 shows a variation calculation of the material exposure for one contact point with and without consideration of the compressive residual stresses near the surface. By neglecting the compressive residual stresses in the case their positive effect on the material exposure is lost, which always leads to a maximal exposure close to the surface. By using the reduced calculation model without consideration of the residual stresses the tooth flank fracture failure, which has its initial crack in greater material depth, cannot be reproduced. This indicates a decisive influence of the residual stresses on the calculation results. Thus fatigue failures due to tooth flank fracture can only be evaluated correctly if the residual stresses are considered during the calculation. As shown in Figure 10 the reduction of the case-hardening depth (curve 1) leads to an increase of the maximum material exposure in greater material depth, whereas the local maximum near the surface remains almost unchanged. Furthermore the maximum of the material exposure shifts towards the surface. Because of the reduced CHD, the core hardness is already achieved in smaller material depth while the hardness near the surface remains the same. An increase of the CHD has the effect that the maximum value of the material exposure is decreased and shifted towards greater depth. All three curves indicate a strong influence of the case hardening depth on the maximum material exposure and its location below the surface. The local peak near the surface is not significantly changed by the CHD variation.

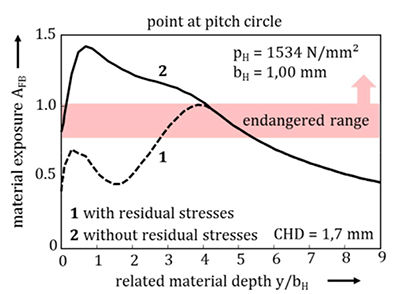
Figure 9 Material exposure curve for one contact point calculated with and without residual stresses (19).

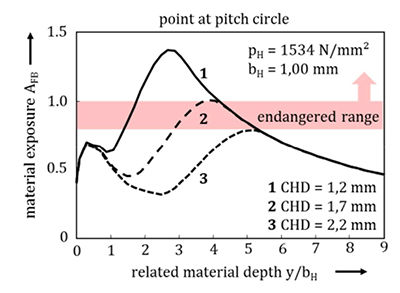
Figure 10 Influence of the CHD on the calculated material exposure (19).

The presented calculation model has the following features and capabilities:

• Check if the maximum material exposure occurs near the surface of the loaded flank or in greater material depth;
• Check if the maximum material exposure is exceeded;
• Predict how deep below the surface an initial crack may occur and consequently which type of failure can be expected;
• Evaluate the risk of tooth flank fracture;

The most decisive influence factors that can be optimized in order to reduce the risk of tooth flank fracture are the gear geometry, represented by the local equivalent radius of curvature, the gear external loads, and the heat treatment.

Validation of the calculation model with test results. A number of tests with test gears especially designed to fail due to tooth flank fracture were carried out in order to prove the applicability of the calculation model, and to verify the critical value of 0.8 of the material exposure. On these test gears the failure of tooth flank fracture was dominant, as it could be reproduced repeatedly during the tests. All failed gears had a maximum material exposure in material depth which was higher than the limit of 0.8. Examinations of the fracture area showed that in almost all cases the initial crack occurred in the casecore transition at non-metallic inclusions, such as aluminum-oxides and/or manganese-sulfides, in an approximate material depth between 0.8 and 1.9 mm. Hereby, the different operating conditions and case-hardening depths of the test gears have to be considered.

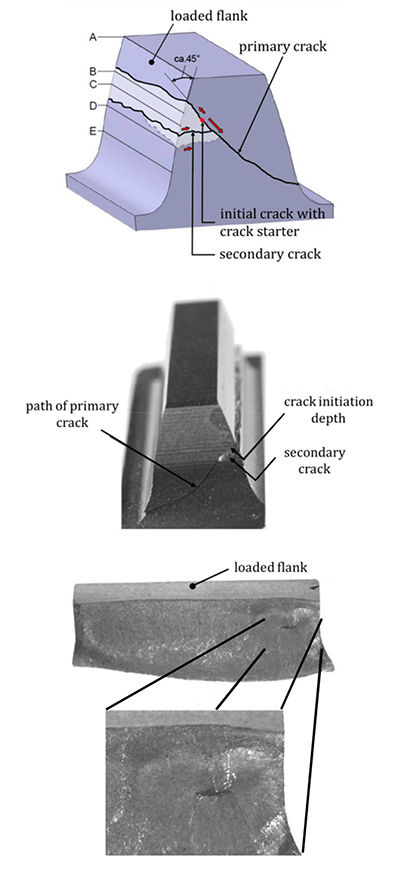
Figure 11 shows example comparison between test result from the gear running tests and the corresponding calculated material exposure. Because of characteristic features, the failure could be identified as tooth flank fracture (Fig. 11, left). The initial crack occurred at flank mid-height in a depth of ca. 1.25 mm below the loaded flank surface, which equals nearly twice the case hardening depth. In Figure 11, right, the calculated material exposure curve for mesh position 5 is plotted over the material depth. The maximum value of AFB, max = 0.92 occurring in a depth of 1.17 mm exceeds the limit of 0.8 and therefore indicates a significant risk of tooth flank fracture. The critical material depth derived from the gear test was very well represented by the calculation as well.

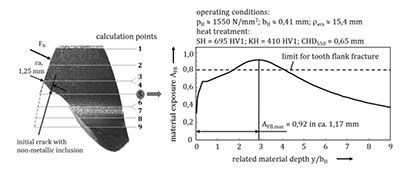
Figure 11 Comparison of test result and calculated material exposure (example for tooth flank fracture).

For comparison, a test gear used for pitting investigations (mn = 5 mm, a = 91.5 mm, z1.2 = 17/18) is shown in Figure 12. The pitting failure, as illustrated on the left, occurred during the test run near the tooth root at mesh position 4. The maximum material exposure of AFB, max = 0.99 in this position is found just below the loaded flank surface, while the material exposure in greater material depth is slightly below the limit for tooth flank fracture of 0.8 and therefore still non-critical regarding tooth flank fracture. Consequently a good correlation between the test and the calculation results is present.

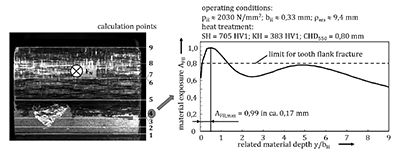
Figure 12 Comparison of test result and calculated material exposure (example for pitting)..

Figure 13 summarizes the results from calculation studies regarding tooth flank fracture, including gearboxes from different applications such as wind turbines, water turbines, highspeed gearboxes and roller mills. For all examined gearboxes the calculated global maximal material exposure is given. The gearboxes on the left failed due to tooth flank fracture and for all gearboxes on the right side no damage or failures due to flank breakage were reported. A good correlation can be found between the calculated maximum material exposures and the observations of the different industrial gearboxes. The comparison confirms tooth flank fracture failures when the critical value of 0.8 of the material exposure is exceeded. All other gearboxes, where no flank breakage occurred, lie beneath 0.8. In general a good applicability of the calculation method could be observed.

Figure 13 Calculated maximum material exposure for different industrial applications (19).

Conclusions

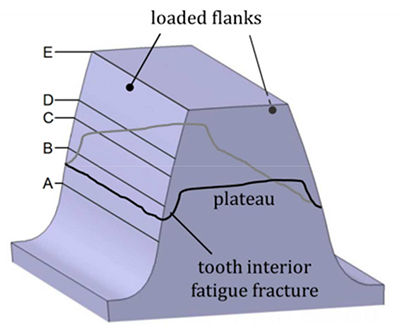
Tooth flank fracture is a sub-surface fatigue failure mode observed on case hardened gears. One characteristic feature of tooth flank fracture is that in comparison to pitting and tooth root breakage, the initial crack can be found below the loaded surface, in greater material depth. Tooth flank fracture leads in almost all cases to the complete breakdown of the gear set. Due to the fact that the crack is propagating inside the material, the failure occurs spontaneously and often without any indications. Standardized calculation methods for pitting and tooth root breakage according to ISO 6336 do not cover this kind of failure. Because of the different failure mechanism, systematic investigations and the development of a new calculation method were of a great importance. The risk of tooth flank fracture can be described with the so called material exposure, which is defined as a relation of the local equivalent shear stress and the local material strength in each volume element in material depth. One distinctive feature of tooth flank fracture is that the crack initiation is normally located below the flank surface in an approximate depth of the case-core transition due to high material exposure — mostly at stress risers like nonmetallic inclusions. With time the initiated crack propagates bi-directionally towards the loaded flank and the tooth fillet of the unloaded flank. When the primary crack reaches the surface, the upper tooth part is separated within a short time due to overload breakage. Both the crack propagation and the overload breakage can be observed on the fracture area — typical for tooth flank fracture. Extensive experimental investigations have shown that the gear geometry, operating conditions, gear material and heat treatment are the decisive factors that influence the risk of tooth flank fracture. A new calculation method was developed in order to calculate the material exposure below the flank surface. It enables the evaluation of the risk of tooth flank fracture and the optimization of the gear design considering all important influence parameters. The validation of the new calculation method shows good correlation with the results from gear running tests and from industrial gear boxes. Because of the fact that tooth flank fracture is a sub-surface fatigue failure that can occur in any application of highly loaded case-hardened gears, the risk should always be considered during the gear design. The new calculation model based on the material exposure below the surface enables the prediction of tooth flank fracture and the optimization of the geometry, material and heat treatment so the risk of a failure can be reduced significantly. Although the newly developed calculation method is based on simplified approaches and assumptions, it allows the evaluation of the tooth flank fracture risk and stays in good correlation with experiences from the field. Goals of future studies are the investigation of further influence factors and their numerical quantification.

References

1. Bauer, E. “Beispiele für Verzahnungsschäden, Ausgehend von Innenliegenden Fehlstellen,” Allianz Report 68, Heft 6, 1995, S. 230–238. 2. Bauer, E. “Flankenbrüche bei Hochleistungsgetrieben,” Allianz Report 2, 1998, S. 79-87.
2. Bretl, N., T. Tobie and P. Oster. “Load Carrying Capacity of Nitrided Gears: Mechanical Properties, Main Influencing Factors and Critical Evaluation of the Application in Gear Transmissions,” Tagung Nitrieren und Nitrocarburieren, Aachen, 2010.
3. (4) DIN 3990: Teil 1-5, Berlin, Beuth Verlag, 1987, Tragfähigkeitsberechnung von Stirnrädern.
4. (5) DNV: Tooth Interior Fatigue Fracture for Case Hardened Gear Wheels & Pinion, Technical Information Newsletter No. 01/2009. 6. (6) Elkholy, A. “Case Depth Requirements in Carburized Gears,” Wear 88, 1983.
5. (7) Hertter, T. “Rechnerischer Festigkeitsnachweis der Ermüdungstragfähigkeit Vergüteter und Einsatzgehärteter Zahnräder,” Dissertation TU München, 2003.
6. (8) ISO 6336: Calculation of Load Capacity of Spur and Helical Gears, Teil 1-5, Genf, 2003.
7. (9) Lang, O.R. “Berechnung und Auslegung induktiv gehärteter Bauteile,” Berichtsband zur AWT-Tagung, Induktives Randschichthärten, Darmstadt, 1989.
8. Mack Aldener, M. “Tooth Interior Fatigue Fracture and Robustness of Gears,” Dissertation KTH Stockholm, 2001.
9. Oster, P. “Beanspruchung der Zahnflanken unter Bedingungen der Elastohydrodynamik,” Dissertation, TU München, 1982.
10. Pederson, R. and R.L. Rice. “Case Crushing of Carburized and Hardened Gears,” Trans. SAE, 1961.
11. Sandberg, E. “A Calcualtion Method for Sub-Surface Fatigue,” International Symposium on Gearing and Power Transmissions, Tokyo, Volume 1, 1981.
12. Sharma, V.K., D.H. Breen and G.H. Walter. “An Analytical Approach for Establishing Case Depth Requirements in Carburized and Hardened Gears,” Trans. of ASME, DETC, Chicago, 1977.
13. Tobie, T., B.-R. Höhn and K. Stahl. “Tooth Flank Breakage — Influences on Subsurface Initiated Fatigue Failures of Case Hardened Gears,” Proceedings of the ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Oregon, 2013.
14. Tobie, T. Zur Grübchen- und Zahnfußtragfähigkeit Einsatzgehärteter Zahnräder, Einflüsse aus Einsatzhärtungstiefe, Wärmebehandlung und Fertigung bei unterschiedlicher Baugröße, Dissertation, TU München, 2001.
15. Wirth, C., B.-R. Höhn and C. Braykoff. “New Methods for the Calculation of the Load Capacity of Bevel and Hypoid Gears,” AGMA Technical Paper 12FTM15, 2012.
16. Witzig, J. Entwicklung eines erweiterten Berechnungsverfahrens zur Ermittlung optimaler Zahnflankentragfähigkeit bis in den Bereich großer Werkstofftiefen, FVA Forschungsheft Nr. 1000, Frankfurt a. M.: Forschungsvereinigung Antriebstechnik e.V., 2011.
17. Witzig, J. “Flankenbruch. Eine Grenze der Zahnradtragfähigkeit in der Werkstofftiefe,” Dissertation TU München, 2012.